Платные прогнозы
Добавил: admin Дата: 14 Ноябрь 2011
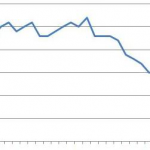
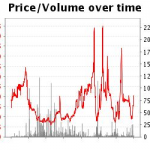
Статистика бесплатного тестового периода:
http://sportodds.ru/p-620
http://sportodds.ru/p-510
Дублирование темы: http://mmgp.ru/showthread.php?t=98504
Кто хочет подписать на получение прогнозов на платной основе оставляйте свои заявки на sportodds@yandex.ru
стоимость 1-ого прогноза – 100р (в случае не прошедшего прогноза 100% стоимости прогноза возвращается на ваш счёт.)
подписка на 10 дней – 1000р (в случае отрицательного баланса 50% стоимости подписки возвращаются на ваш счёт.)
подписка на 1 месяц – 3000р (в случае отрицательного баланса 60% стоимости подписки возвращаются на ваш счёт.)
Платные прогнозы будут появляться за 1 минуту +- до начала матча!
73) футбол 05.08.11 20:00 Санкт-Паули — Алемания ...